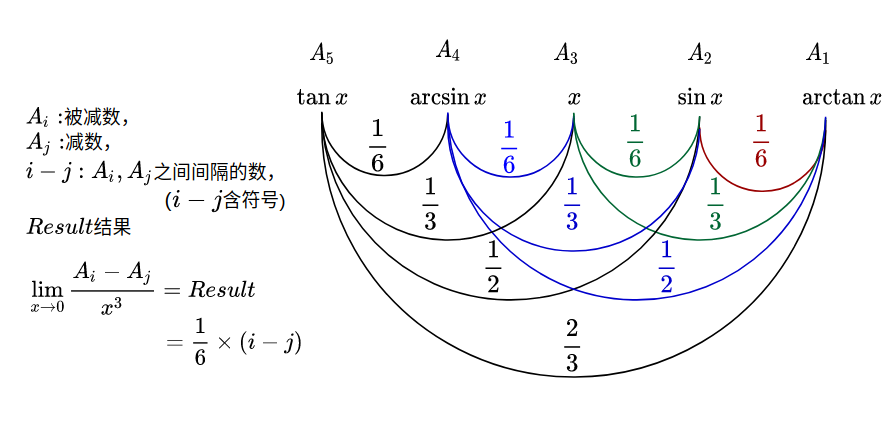
三角函数之差与三次函数的等价无穷小关系
在之前最开始常老师带的高数时有提到关于三角函数之差与三次函数的等价无穷小间的关系,后来高数竞赛也零零散散用到一些,汤家凤的课程也一下有这样的关系,后来把所有组合全部走了一遍,发现之间还存在进一步的记忆规律和对称性,此篇小记一下。
- 行文
- 引入
- 准备
- 组合
- 总结
引入
- $x\to0$时,$\sin{x}\sim\tan{x}\sim\arcsin{x}\sim\arctan{x}\sim x$是等价无穷小
- 三角函数$\sin{x},\tan{x},\arcsin{x},\arctan{x}$和一次函数$x$两两相减与在$x\to0$时与$x^3$是同阶无穷小,
- 本文讨论具体无穷小的数值关系。
- 即$\lim_{x\to0}\frac{A-B}{x^3}=Resault,(A,B\in {\sin{x},\tan{x},\arcsin{x},\arctan{x},x})$
准备
判断大小
根据函数图像
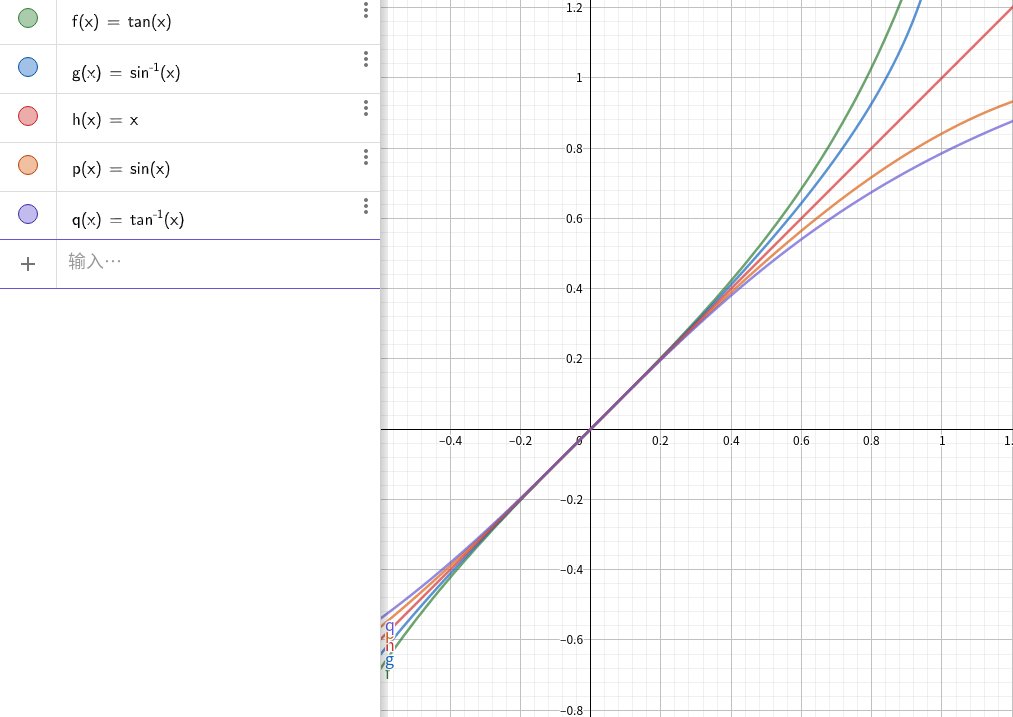
得,在$x\to0$时$\tan{x}>\arcsin{x}>x>\sin{x}>\arctan{x}$
则最终结果$\lim_{x\to0}\frac{\tan{x}-x}{x^3}=Resault>0$以此类推,可以得到其他结果正负
思路
可以先求出与$x$差的关系,再利用$A-B=A-x-(B-x)$拆开求
分母是$x^3$三次,如果分子求导不引入新的分母成分,则三次洛必达再代入一定可以解出来
不引入分母是指$(\sin{x})’=\cos{x},(\tan{x})’=\sec^2{x}$,而引入分母是指$(\arcsin{x})’=\frac{1}{\sqrt{1+x^2}},(\arctan{x})’=\frac{1}{1+x^2}$
如果含有$\arcsin{x}$尽量避免使用洛必达,而是使用$x=\sin{t}$进行代换
如果可以凑分子(母)含有$\cos{x},1+x^2$也是可以的,如果此时分母(子)如果也是(或者可以拆成)二次的,则可以拆开用等价无穷小
后来想到,可以用泰勒展开式更加清晰明了 参考
组合
主线
- $x$减去其他四项
- $x-\sin{x}$
$\lim_{x\to0}\frac{x-\sin{x}}{x^3}=^{(1)}\lim{x\to0}\frac{1-\cos{x}}{3x^2}=^{(2)}\lim{x\to 0}\frac{\frac{1}{x^2}}{3x^2}=\frac{1}{6}$
(1)洛必达
(2)等价无穷小$1-\cos{x}\sim\frac{x^2}{2}$
- $x-\tan{x}$
$\lim_{x\to0}\frac{x-\tan{x}}{x^3}=^{(1)} \lim{x\to 0}\frac{1-\sec^2{x}}{3x^2}=^{(2)} \frac{-\tan^2{x}}{3x^2}=^{(3)}-\frac{1}{3}$
(1)洛必达
》(2)三角恒等代换
(3)等价无穷小
- $x-\arcsin{x}$
$\lim_{x\to0}\frac{x-\arcsin{x}}{x^3}=^{(1)x=\sin{t}}\lim{t\to 0}\frac{\sin{t}-t}{\sin^3{t}}=^{(2)}\lim{t\to 0}\frac{\sin{t}-t}{t^3}=^{(3)}\frac{\cos{t}-1}{3t^2}=^{(4)}-\frac{1}{6}$
》(1)三角代换
(2)分子等价无穷小$\sin{x}\sim x$
(3)洛必达
(4)等价无穷小
- $x-\arctan{x}$
$\lim_{x\to0}\frac{x-\arctan{x}}{x^3}=^{(1)}\lim{x\to 0}\frac{1-\frac{1}{1+x^2}}{3x^2}=^{(2)}\lim{x\to 0}\frac{1}{3(1+x^2)}_=^{(3)}\frac{1}{3}$
(1)洛必达
(2)约分,因为$x\to 0$,所以取不到0,所以含有$x$可以约分,约分就是除以一个不为0的数
(3)直接代入$x=0$
副线
- 通法
- 以$x$为中介拆开求,???同次可以拆开,也就是说已经提前知道是同次了
- 以$\sin{x}-\arctan{x}$为例,其余情况在文尾结论处给出
$\lim_{x\to 0}\frac{\sin{x}-\arctan{x}}{x^3}=^{(1)}\lim{x\to 0}(\frac{\sin{x}-x}{x^3}-\frac{\arctan{x}-x}{x^3})_=^{(2)}-\frac{1}{6}-(-\frac{1}{3})=\frac{1}{6}$
- 其他不同方法
$\lim_{x\to 0}\frac{\sin{x}-\tan{x}}{x^2}=^{(1)}\frac{tan{x}}{x}\cdot \frac{\cos{x}-1}{x^3}=^{(2)}1\cdot (-\frac{1}{2})=-\frac{1}{2}$
》(1)凑$\cos{x}-1$和$x^2$
(2)等价无穷小
$\lim_{x\to0}\frac{x-\arctan{x}}{x^3}=^{(1)}\frac{1-\frac{1}{1+x^2}}{3x^2}=^{(2)}\lim_{x\to 0}(\frac{\cos{x}-1}{3x^2}-\frac{\frac{1}{1+x^2}-1}{3x^2})=^{(3)}\lim{x\to 0}(\frac{\cos{x}-1}{3x^2}-\frac{x^2}{(1+x^2)(3x^2)})=^{(4)}\lim{x\to0}\frac{-\frac{1}{2}x^2}{3x^2}+\frac{1}{3}=\frac{1}{6}$
(1)洛必达
》(2)插入1凑$\cos{x}-1$,都是二次的,分子两部分可以拆开
(3)后部分变形化简
(4)前部分等价无穷小,后部分极限是0取不到0可以约分,约分后直接代入$x=0$
$\lim_{x\to0}\frac{x-\arctan{x}}{x^3}=^{(1)}\frac{1-\frac{1}{1+x^2}}{3x^2}=^{(2)}\lim_{x\to 0}(\frac{\cos{x}-1}{3x^2}-\frac{\frac{1}{1+x^2}-1}{3x^2})=^{(3)} \frac{-\sin{x}-\frac{-2x}{(1+x^2)^2}}{6x}=^{(4)}\frac{-\cos{x}+\frac{2(1+x^2)^2-(2x)^2\cdot 2(1+x^2)}{(1+x^2)^4}}{6}_=^{(5)}\frac{-1+\frac{2}{1}}{6}\frac{1}{6}$
(1)洛必达
》(2)插入1凑$\cos{x}-1$,都是二次的,分子两部分可以拆开
》(3)洛必达,分母三次,最多洛必达三次一定可以,最后会代入0,所以再复杂也不怕
(4)洛必达
(5)前部分,后部分,都直接代入$x=0$
总结
根据函数图像得大小关系
$\tan{x}>\arcsin{x}>x>\sin{x}>\arctan{x}$
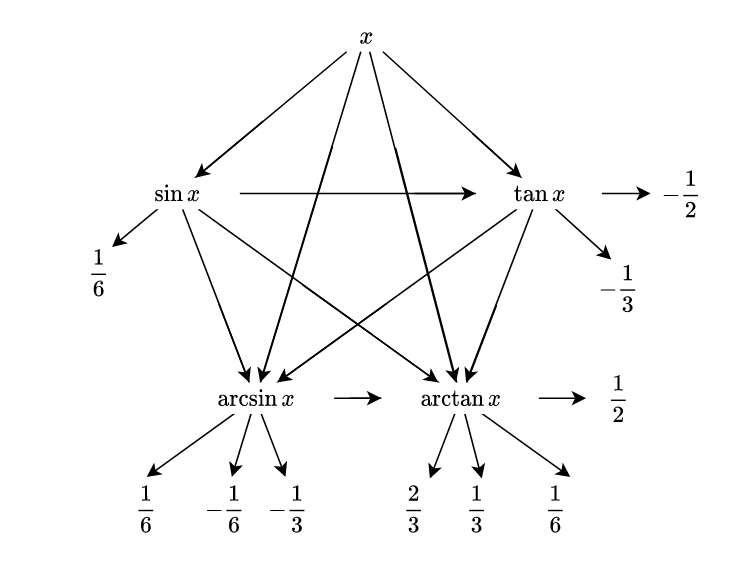
根据组合求数值
观察结果数值规律
数值为
- $\frac{1}{6}=\frac{1}{6}\times1$
- $\frac{1}{3}=\frac{1}{6}\times2$
- $\frac{1}{2}=\frac{1}{6}\times3$
- $\frac{2}{3}=\frac{1}{6}\times4$
结合大小得出结论
- 设
- $A_5=\tan{x},A_4=\arctan{x},A_3=x,A_2=\sin{x},A_1=\arctan{x}$
- $i,j\in{1,2,3,4,5}$
- 则
- $\lim_{x\to 0}\frac{A_i-A_j}{x^3}=\frac{1}{6}\times(i-j)$
- 设
即:相邻的两个之差与$x^3$比的极限是$\frac{1}{6}$,隔一个则是$\frac{1}{6}\times 2$